이상기체의 혼합물의 경우 열역학적 성질은 어떻게 표현되는지 알아보자. 먼저 깁스의 정리를 알고 있어야한다.
- 깁스의 정리
이상기체 상태 혼합물에서 한 구성성분의 부분 몰성질(부피는 제외)은 혼합물과 같은 온도 및 혼합물에서의 그 성분의 분압과 같은 압력에서 순수 이상기체 상태인 그 성분의 상응하는 몰 성질과 같다. 식으로 표현하면 아래와 같다.

글로만 읽으면 이해하기 어려운데 예시를 들어보자. 이상기체 A, B, C가 섞인 혼합물이 압력 P와 온도 T인 상태에 있다고 가정한다. 깁스의 정리란 혼합물에서 A의 부분 몰성질(압력 P, 온도 T인 경우)은 순수한 A의 몰성질(부분압력 Pa, 온도 T인 경우)과 동일하다는 것이다. 부분 몰성질에 돌턴의 분압법칙을 적용한다고 생각하면 그나마 이해가 쉬울 것이다(이해 안된다면 죄송합니다ㅠ) 이 정리로부터 이상기체 혼합물의 열역학적 성질을 유도할 수 있다.
유도에 앞서 이상기체 계에서 내부에너지(U)와 엔탈피(H)는 온도만의 함수이고, 엔트로피(S), 깁스에너지(G), 헬름홀츠에너지(A)는 온도와 압력의 함수라는 것을 알아야 한다.
1. 내부에너지와 엔탈피

위 식과 아래 식 모두 첫번째 등호는 깁스의 정리에 의해 성립한다. 두번째 등호는 내부에너지와 엔탈피는 모두 온도만의 함수이기 때문에 압력이 달라져도 온도가 일정하면 같은 값을 가지기 때문에 등호가 성립한다. 즉 내부에너지와 엔탈피는 온도 T와 압력 P에서 부분 몰성질과 순수성분 몰성질이 같다는 것을 알 수 있다.
2. 엔트로피, 깁스에너지, 헬름홀츠에너지
깁스의 정리에 의해 아래 식들이 성립한다.

이상기체인 경우, 엔트로피는 아래와 같이 표현할 수 있고, 최종적으로 부분 몰성질과 순수성분 몰성질의 관계를 나타낸 식은 아래와 같다. 나머지 열역학적 성질도 유도한 결과는 아래와 같다.
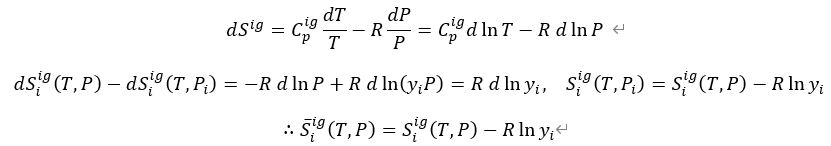

또한 열역학적 성질의 전미분을 이용해 아래와 같은 식을 유도할 수 있다.

이 식을 이용하면 혼합 전후 열역학적 성질의 차이를 계산할 수 있다. 혼합 전후 차이는 아래와 같은 식으로 계산한다.

이 식에서 앞의 항은 혼합 후 혼합물의 몰성질을 의미하고, 뒤의 항은 혼합 전 순수한 물질의 몰성질을 의미한다. 이 식을 열역학적 성질에 모두 적용해본다.



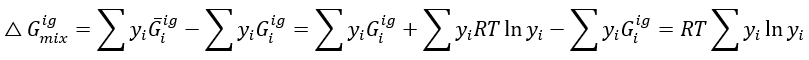

따라서 이상기체의 엔탈피와 내부에너지는 혼합에 따른 변화가 없으며 엔트로피, 깁스에너지, 헬름홀츠에너지는 혼합에 따른 변화가 몰분율에 따라 달라진다는 것을 알 수 있다. 이것이 결론이니 유도과정이 이해가 안된다면 가장 마지막 수식의 결과만이라도 챙겨가자.
'필수개념 > 화공열역학' 카테고리의 다른 글
| 비압축성 유체의 열역학적 성질 (0) | 2023.02.06 |
|---|
